无监督聚类最佳个数选取
背景
聚类(Clustering) 是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。在聚类分析的时候确定最佳聚类数目是一个很重要的问题,这无论是划分聚类还是层次聚类等,都会涉及的问题,接下来我们就此问题展开讨论。
判定最佳聚类个数方法
###读取数据,后续方法都已该数据格式为准(列为样本,行为变量)对行变量进行聚类个数选择
data <- read.table("Demo_clust.txt",header = T,row.names = 1,check.names = F,sep="\t",quote="",stringsAsFactors = F)
data1 <- data.frame(scale(data[,-1]))
head(data1)
K1 K2 K3 C1 C2 C3
ENSG00000001461 -0.04413945 -0.04547074 -0.04476907 -0.05349480 -0.05388352 -0.05417346
ENSG00000001630 -0.04421514 -0.04556221 -0.04486315 -0.05408137 -0.05441789 -0.05464083
ENSG00000002549 -0.04409769 -0.04545400 -0.04477969 -0.05336693 -0.05369686 -0.05397042
ENSG00000003989 -0.04416451 -0.04551200 -0.04482226 -0.05365372 -0.05402450 -0.05420352
ENSG00000004139 -0.04422096 -0.04556918 -0.04487408 -0.05412167 -0.05448478 -0.05468413
ENSG00000004700 -0.04415662 -0.04550351 -0.04482669 -0.05365463 -0.05401998 -0.05409201mclust (Model-based clustering)
mclust在R语言上实现了基于高斯有限混合模型的聚类,分类和密度估计分析,并且还有专门的可视化函数展示分析结果。对于具有各种协方差结构的高斯混合模型,它提供了根据EM算法的参数预测函数。它也提供了根据模型进行模拟的函数。还提供了一类函数,整合了基于模型的层次聚类,混合估计的EM算法,用于聚类、密度估计和判别分析中综合性策略的贝叶斯信息判别标准。最后还有一类函数能够对聚类,分类和密度估计结果中的拟合模型进行可视化展示。
原理:和其他基于模型的方法类似,Mclust假设观测数据是一个或多个混合高斯分布的抽样结果,Mclust就需要根据现有数据去推断最优可能的模型参数,以及是由 q几组分布抽样而成。mclust一共提供了14种模型**(见下表)**,可以用?mclustModelNames查看mclust提供的所有模型。
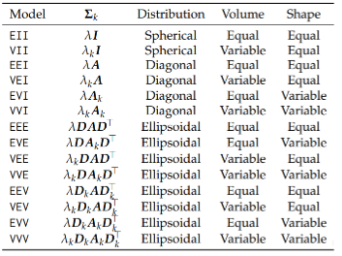
mclust默认得到14种模型1到9组的分析结果,选择其中BIC最大的模型和分组作为最终的结果。
mclust包里的“BIC值”,并非BIC(Bayesian Information Criterion ):贝叶斯信息判别标准,是作者自己定义的BIC,这里的BIC与极大似然估计成正比,所以这里是BIC值越大越好,与贝叶斯信息准则值越小模型越好的结论并不冲突
以下是实操:
# 安装并加载mclust包
install.packages("mclust")
library(mclust)
# mclust聚类个数选择
mod <- Mclust(scale(data1))
mod
'Mclust' model object: (VEV,7)
Available components:
[1] "call" "data" "modelName" "n" "d" "G" "BIC"
[8] "loglik" "df" "bic" "icl" "hypvol" "parameters" "z"
[15] "classification" "uncertainty"
# 可根据mod$G返回判断的最佳聚类个数
> mod$G
[1] 7
# 根据mod$classification返回聚类详细信息
> mod$classification
ENSG00000001461 ENSG00000001630 ENSG00000002549 ENSG00000003989 ENSG00000004139 ENSG00000004700 ENSG00000004864
3 1 3 3 1 3 3
ENSG00000005102 ENSG00000005187 ENSG00000005189 ENSG00000005810 ENSG00000006125 ENSG00000006432 ENSG00000006459
3 3 3 3 4 1 1
ENSG00000006607 ENSG00000006611 ENSG00000006747 ENSG00000007202 ENSG00000007237 ENSG00000007306 ENSG00000007923
3 4 3 3 1 3 2
# 使用plot.Mclust可视化BIC变化曲线
plot.Mclust(mod,what = 'BIC')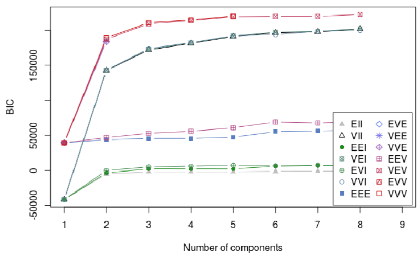
参考文献:Scrucca, Luca et al. “mclust 5: Clustering, Classification and Density Estimation Using Gaussian Finite Mixture Models.” The R journal vol. 8,1 (2016): 289-317.
Nbclust
类似mclust,也是自己定义了几十种评估指标,之后遍历每一个设定的聚类数目,通过这些指标分别在聚类数为多少时达到最优,最后选择指标支持数最多的聚类数目作为最佳聚类数目。大体过程是用某种已有的聚类算法或者是划分类别的方法如:Kmeans,Ward(最小化类内方差),Single(最小距离),Complete(最大距离)和Average(平均距离)等,对每一个设定的类别个数进行聚类,得出聚类结果后用评估指标评估。
以下是实操:
# 安装并加载Nbclust包
install.packages("NbClust")
library(NbClust)
# NbClust聚类个数选择,distance距离计算方法,min.nc最小聚类个数,max.nc最大聚类个数,method聚类方法,可使用?NbClust查看相关用法
nb_clust <- NbClust(data1, distance = "euclidean", min.nc=2, max.nc=15, method = "kmeans")
# 根据nb_clust$Best.nc返回投票结果
nb_clust$Best.nc[1,]
KL CH Hartigan CCC Scott Marriot TrCovW TraceW Friedman Rubin Cindex
2 2 3 2 5 5 5 3 8 3 10
DB Silhouette Duda PseudoT2 Beale Ratkowsky Ball PtBiserial Frey McClain Dunn
2 2 3 3 3 2 3 2 NA 2 2
Hubert SDindex Dindex SDbw
0 10 0 10
# 返回每个聚类个数下,指标投票数量
NC <- table(nb_clust$Best.n[1,])
NC
0 2 3 5 8 10
2 9 7 3 1 3
# 可视化每个聚类个数下,指标投票数量,可见投票最多的聚类个数为2
barplot(NC, xlab="Number of Clusters", ylab="Number of Criteria")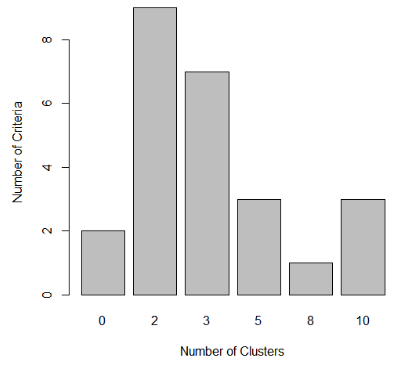
参考文献:Charrad, M., . N. Ghazzali, V. Boiteau, and A. Niknafs. “NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set”. Journal of Statistical Software, 61,6 (2014): 1-36.
elbow组内平方误差和——拐点图
拐点图是用一个最简单的指标——sum of squared error (SSE)组内平方误差和来确定最佳聚类数目。
以下是实操:
# 安装并加载factoextra包
install.packages("factoextra")
library(factoextra)
# 绘制拐点图,wss(for total within sum of square),可以看出曲线的拐点为2
fviz_nbclust(data1, kmeans, method = "wss")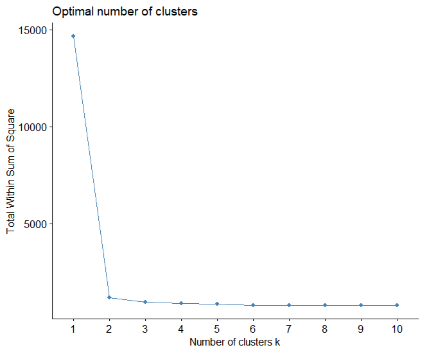
Gap Statistic
上面我们提到了WSSE组内平方和误差,该种方法是通过找“肘点”来找到最佳聚类数,肘点的选择并不是那么清晰,因此斯坦福大学的Robert等教授提出了Gap Statistic方法。
Gap值计算公式:
通过这个式子来找出Wk跌落最快的点,Gap最大值对应的k值就是最佳聚类数。
以下是实操:
# 安装并加载cluster、factoextra包
install.packages("cluster")
install.packages("factoextra")
library(cluster)
library(factoextra)
# 聚类个数选择,给出最佳聚类个数为2
gap_clust <- clusGap(data1, kmeans, 10, B = 100, verbose = interactive())
gap_clust
Clustering Gap statistic ["clusGap"] from call:
clusGap(x = data1, FUNcluster = kmeans, K.max = 10, B = 100, verbose = interactive())
B=100 simulated reference sets, k = 1..10; spaceH0="scaledPCA"
--> Number of clusters (method 'firstSEmax', SE.factor=1): 2
logW E.logW gap SE.sim
[1,] 5.033634 9.956219 4.922585 0.008375066
[2,] 4.391552 9.343772 4.952220 0.008229527
[3,] 4.079586 9.032698 4.953112 0.007896211
[4,] 3.933550 8.841375 4.907825 0.006300275
[5,] 3.790862 8.714457 4.923595 0.006245972
[6,] 3.595483 8.625568 5.030086 0.011053841
[7,] 3.428855 8.563961 5.135107 0.011684481
[8,] 3.355988 8.513325 5.157338 0.009182897
[9,] 3.291024 8.464354 5.173330 0.008347755
[10,] 3.215980 8.416334 5.200354 0.008076932
# 通过fviz_gap_stat函数可视化结果(可能由于数据原因导致模型结果不准)
fviz_gap_stat(gap_clust)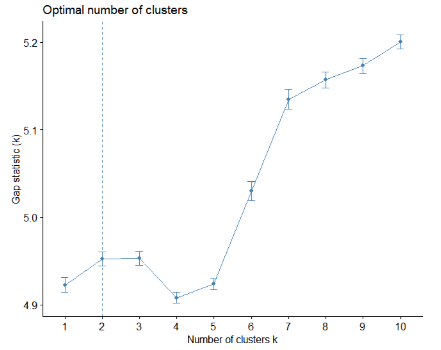
参考文献:Tibshirani R, Walther G, Hastie T. Estimating the number of clusters in a data set via the gap statistic[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2001, 63(2): 411-423.
轮廓系数(Average silhouette method)
轮廓系数是类的密集与分散程度的评价指标。
a(i)是测量组内的相似度,b(i)是测量组间的相似度,s(i)范围从-1到1,值越大说明组内吻合越高,组间距离越远——也就是说,轮廓系数值越大,聚类效果越好。
以下是实操:
# 安装并加载cluster、factoextra包
install.packages("cluster")
install.packages("factoextra")
library(cluster)
library(factoextra)
# 绘制各聚类个数下的轮廓系数图,可看出最佳聚类个数为2
fviz_nbclust(data1, kmeans, method = "silhouette")
# 之后和通过挑选的最佳聚类个数,绘制轮廓图(由于本数据不好,这里的结果图以其他数据为例)
km.res = kmeans(data1, 2, nstart = 1000)
sil = silhouette(km.res$cluster, dist(data1))
rownames(sil) = rownames(data1)
head(sil[, 1:3])
cluster neighbor sil_width
ENSG00000001461 1 2 0.9992706
ENSG00000001630 1 2 0.9992719
ENSG00000002549 1 2 0.9992691
ENSG00000003989 1 2 0.9992713
ENSG00000004139 1 2 0.9992714
ENSG00000004700 1 2 0.9992709
fviz_silhouette(sil)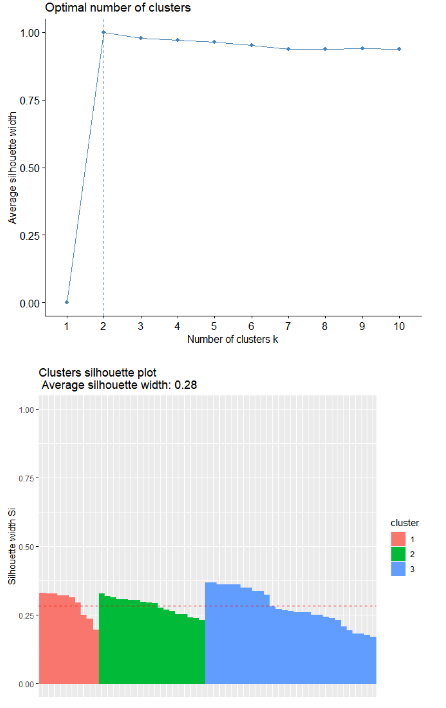
Calinsky criterion
Calinski-Harabasz准则有时称为方差比准则 (VRC),它可以用来确定聚类的最佳K值。评估标准定义如下:
其中,K是聚类数,N是样本数(在这里是变量个数),SSB是组与 组之间的平方和误差,SSw是组内平方和误差。因此,如果SSw越小、SSB越大,那么聚类效果就会越好,即Calinsky criterion值越大,聚类效果越好。
以下是实操:
# 安装并加载vegan包
install.packages("vegan")
library(vegan)
# calinski值计算
ca_clust <- cascadeKM(data1, 1, 10, iter = 100)
ca_clust$results
1 groups 2 groups 3 groups 4 groups 5 groups 6 groups 7 groups 8 groups 9 groups 10 groups
SSE 14640 1195.359 954.1942 894.112 847.3067 806.9225 44.81731 790.3347 782.5748 780.0961
calinski NA 27432.336 17483.8604 12488.639 9913.4703 8348.6440 132109.20365 6090.7712 5383.0732 4799.0424
# 返回calinski最大值时的k值,最佳聚类个数为7
calinski.best <- as.numeric(which.max(ca_clust$results[2,]))
calinski.best
[1] 7
# 结果可视化
plot(ca_clust, sortg = TRUE, grpmts.plot = TRUE)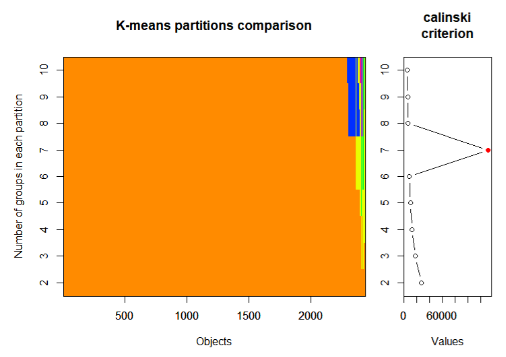
参考:Calinski-Harabasz criterion clustering evaluation object - MATLAB - MathWorks 中国
参考文献:Calinski, T., and J. Harabasz. “A dendrite method for cluster analysis.” Communications in Statistics. Vol. 3, No. 1, 1974, pp. 1–27.
PAM (Partitioning Around Medoids) 围绕中心点的分割算法
k-means算法取得是均值,因此异常点对该算法影响很大,很可能将异常点聚为一类,PAM算法则避免了这种情况,也叫k-medoids clustering。
原理:选用簇中位置最中心的对象,试图对n个对象给出k个划分;代表对象也被称为是中心点,其他对象则被称为非代表对象;最初随机选择k个对象作为中心点,该算法反复地用非代表对象来代替代表对象,试图找出更好的中心点,以改进聚类的质量;在每次迭代中,所有可能的对象对被分析,每个对中的一个对象是中心点,而另一个是非代表对象。对可能的各种组合,估算聚类结果的质量;一个对象Oi可以被使最大平方-误差值减少的对象代替;在一次迭代中产生的最佳对象集合成为下次迭代的中心点。kmedoids算法比kmenas对于噪声和孤立点更鲁棒,因为它最小化相异点对的和(minimizes a sum of pairwise dissimilarities )而不是欧式距离的平方和(sum of squared Euclidean distances.)。一个中心点(medoid)可以这么定义:簇中某点的平均差异性在这一簇中所有点中最小。
以下是实操:
# 安装并加载fpc包
install.packages("fpc")
install.packages("cluster")
library(fpc)
library(cluster)
# 计算最佳k值
pamk.best <- pamk(data1)
pamk.best$nc
[1] 2
# 可视化(由于本数据不好,这里的结果图以wine数据集为例)
clusplot(pam(data1, pamk.best$nc))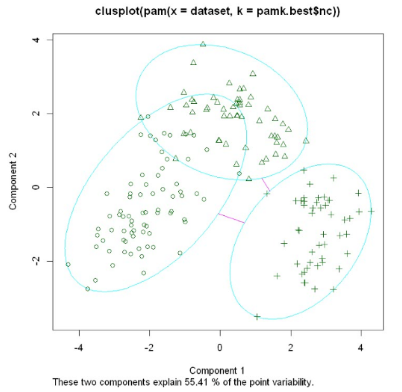
参考文献:Hae-Sang Park, Chi-Hyuck Jun, A simple and fast algorithm for K-medoids clustering, Expert Systems with Applications, Volume 36, Issue 2, Part 2, 2009, Pages 3336-3341, ISSN 0957-4174, https://doi.org/10.1016/j.eswa.2008.01.039.