聚类一致性
为了保证聚类结果的稳定或者说是一致性,分型算法通常会运行多次,用于评估聚类的稳定性(例如nmf函数的nrun参数,ConsensusClusterPlus函数的reps参数均可控制运行次数)
比较好理解的如ConsensusClusterPlus函数默认每次随机选取80%的样本进行分型(即重采样);而NMF则基于不同的随机种子,产生不同的分型结果;
一致性矩阵
假设有D1,D2...Dn这N个样本,那么consensus matrix是NxN 的方阵,如下:
| D1 | D2 | D3 | ... | Dn | |
|---|---|---|---|---|---|
| D1 | C11 | C12 | C13 | ... | C1n |
| D2 | C21 | C22 | C23 | ... | C2n |
| ... | ... | ... | ... | Cij | ... |
| Dn | Cn1 | Cn2 | Cn3 | ... | Cnn |
Cij 代表的是在多次的聚类结果中,样本Di 和样本Dj 被划分到同一类的概率(该值在0-1之间,该值越大表示样本ij被划分为同一类的概率越大)。
相关信息
对consensus matrix再做一次聚类,即可方便地对其可视化
下图中,不同的k值表示不同亚型数量下对应的聚类一致性热图。
热图行和列均为样本,热图上侧color bar为样本对应的亚型注释,热图颜色深浅表示聚类一致性高低(即多次随机过程中,样本被聚类在一起的概率),热图中相同亚型内颜色越深,不同亚型间颜色越浅表示聚类一致性越高;

评价指标-一致性聚类算法
聚类一致性热图直观地可视化了不同K值下的聚类一致性,但例如上文K=3 & k=5的热图就难以区分优劣,因此可借助特定算法将consensus matrix量化为分型评价指标。
Consensus Cumulative Distribution Function(一致性累计分布图)是Consensus Cluster算法最经典的分型评价指标之一,分别将不同K值下的consensus matrix转化为向量,绘制累积分布图即可得到如下图像:
相关信息
从绘制原理即可看出,为什么通常选取下降坡度相对小的CDF曲线最优最优的分型数量K。因为,坡度越平缓说明consensus matrix中,0 & 1之外的值就越少。当consensus matrix只有0 & 1时,坡度与x轴平行,聚类一致性达到最优。
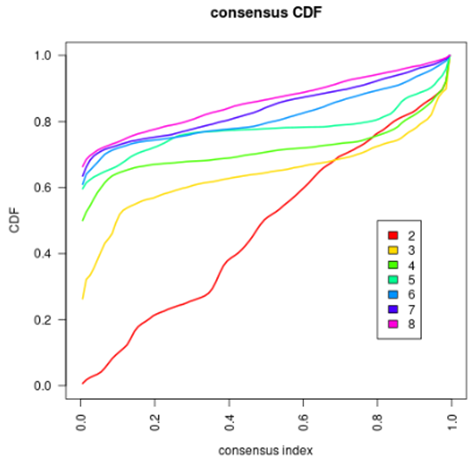
#results为ConsensusClusterPlus结果对象,基于以下代码可实现手动绘制一致性累计分布图
bb <- do.call(rbind, lapply(2:8, function(x){
aa <- as.numeric(results[[x]]$consensusMatrix)
df_2 <- data.frame(Consensus_index = aa, K = rep(as.character(x), length(aa)) )
return(df_2)
}))
ggplot(bb, aes(Consensus_index, colour = K)) +
stat_ecdf(geom = "step") + ylab("CDF") +
theme_bw() +
theme(panel.grid.major=element_blank(),panel.grid.minor=element_blank()) +
theme(axis.text = element_text(size = 16),axis.title=element_text(size = 16)) + labs(title="")Delta Area Plot(CDF 曲线下面积的相对变化折线图) 展示了 k 和 k-1 相比CDF曲线下面积的相对变化。当k = 2时,因为没有k=1,所以第一个点表示的是k=2时CDF曲线下总面积。
通常选取折线拐点作为最佳K值,也有研究者选择曲线下面积变化小的点作为最佳K值。(事实上,它们的原理大同小异)
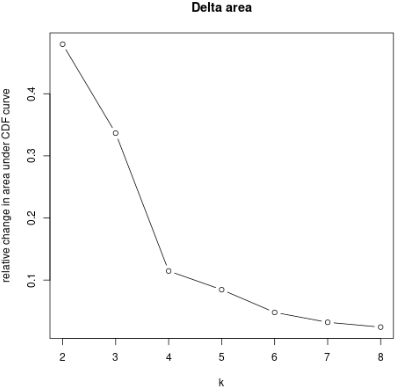
综上所述,Consensus CDF & Delta Area Plot 都是对consensus matrix进一步处理得到的比热图更直观的评价指标。
评价指标-NMF算法
首先,如下图,NMF算法会计算每个样本的轮廓系数(Silhouette coefficient),并在聚类一致性热图上作为color bar注释呈现;
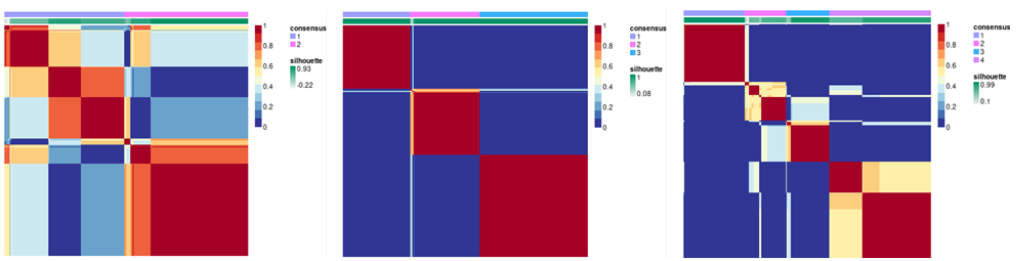
轮廓系数基于距离矩阵计算;用来量化一个目标对于目标所在簇与其他簇之间的相似性(-1~1);值越大表明目标与自己所在簇的匹配度越高,与其他簇的匹配度越低,聚类结果越好;
计算公式如下:
假设样本分成K个簇,a(i)是样本i与同簇其它样本的平均距离;a(i)越小聚类结果越好;
b(i)是样本i与其它簇其它样本的平均距离;b(i)越大聚类结果越好;
s(i)是轮廓系数,越大越好;
每个K的轮廓系数怎么算?
每个K下所有样本的轮廓系数均值;
如下图,为什么NMF输出三条轮廓系数折线?分别是什么?
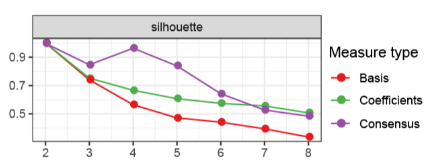
未查到官方说明,以下解释为个人基于经验做出的猜测:
1.由于轮廓系数基于距离矩阵计算,那么三条轮廓系数对应三种不同的距离矩阵;
2.紫色的Consensus最好理解,对应consensus matrix;
3.如下图,由于NMF的算法原理是将V矩阵分解为W & H矩阵(即_Basis matrix &_ coefficient matrix),基于两个矩阵根据上述公式计算即可;
Membership Score
Membership Score是NMF算法特有的每个样本的评价指标,同样用于评估每个样本划分为当前亚型的准确性。它由上文的H矩阵计算得来,原理比轮廓系数更简单:
"Calculated a cluster membership score as the maximal fractional score of the corresponding column in matrix H"
有文献会基于membership score过滤样本,得到亚型核心样本集合:We defined a cluster core as the set of samples with cluster membership score > 0.5
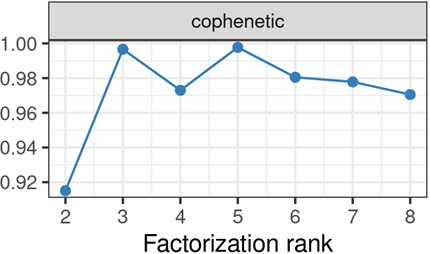
共表象系数-cophenetic coefficient
共表象系数全称共表象相关系数(Cophenetic Correlation Coefficient),用于评估样本聚类稳定性的指标,也是NMF算法最常用的确定最优聚类数量的指标。
在NMF算法中,首先基于consensus matrix得到距离矩阵(Distance matrix) & 共表象矩阵(Cophenetic Matrix),然后做相关得到共表象相关系数;
距离矩阵--可以是简单的欧式距离矩阵;
共表象矩阵--是聚类树状图上,任意两样本合并为一类的纵向距离(the dendrogrammatic distance between the model points. This distance is the height of the node at which these two points are first joined together.)
将上述两个矩阵转化为向量,计算相关性,即可得到共表象相关系数,如下图:
研究者Brunet建议选取曲线下降最大的前点K值作为最优聚类数;_(_PNAS. 2004, 101(12):4164-9. doi: 10.1073/pnas.0308531101.)