stats

Cox回归

Jeason

1893字约6分钟

stats

2018-04-23

Cox回归分析是在生存分析中最常用的影响因素分析，回归模型的前提假设只有一个：分析的因素必须满足比例风险假设，即协变量不随时间的变化而变化。

Cox比例风险模型

Cox回归模型建模的主要对象是危险率（Hazard Rate），记作 $h(t)$ ，它的基本形式：

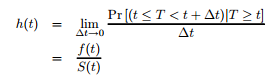
它表示已生存到时间 $t$ 的观察对象在t时刻的瞬时发生事件的概率，值为非负数。当 $Δt=1$ 时，此时风险函数表示的就是时刻t存活的个体在此后一个单位死亡概率。

Cox回归的假设是 $h$ 满足这样的分布：

其中 $h_0(t)$ 我们不要去管它,，表示的是基线风险，即协变量为0时的风险率。对于两个对象，它们危险率的比值（Hazard Ratio）是和 $h_0(t)$ 无关的。

对于每一个因素，如果回归系数的检验检验p值小于给定阈值，那么它的回归系数如果为正，该因素为风险因素，否则为保护因素（不利因素）。当确定该因素确实影响生存之后，影响力的大小可以用HR（hazard ratio）来表示。HR表示该影响因素增加一个单位风险率相对于原来增加多少倍。

总结起来就是：

P<0.05,β>0，HR>1(95%CI >1)，说明变量X增加时，危险率增加，即X是危险因素；
P<0.05,β<0，HR<1(95%CI <1)，说明变量X增加时，危险率下降，即X是保护因素；
P=0.05,β较大可能=0，HR较大可能=1，说明变量X增加时，危险率不变，即X是危险无关因素。

比例风险的假设的检验

该假设主要用于评估协变量是否可以用于cox风险回归模型。但是，一般都不需要进行评估。

判断一个变量是否满足比例风险模型假设有以下三种方式：

如果协变量为类协变量（即category var），那么每组别的K-M生存曲线无交叉，则满足比例风险假设；
以生存时间t为横轴，对数对数生存率ln[-ln(p)]为纵轴，绘制分类变量的每一组别的生存曲线，如果各组别对应的曲线直观上平行，则满足风险比例条件。
对于连续型协变量，可将每个协变量与对数生存时间的交互项X*ln(t)放入回归模型中，如果该将互相项没有统计学意义，则满足风险比例假设，如：

当分析按比例风险的假定条件不成立是，可采用两种方法来解决：

将这种不满足假定的协变量作为分层变量，然后再用其余变量进行多元Cox回归模型分析。（分层分析）
使用其他的参数模型。

R语言实现

survival用于计算生存分析
survminer用于可视化生存分析结果

单因素cox分析

library(survival)
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)

Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
      coef exp(coef) se(coef)     z      p
sex -0.531     0.588    0.167 -3.18 0.0015
Likelihood ratio test=10.6  on 1 df, p=0.00111
n= 228, number of events= 165 

summary(res.cox)

Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
  n= 228, number of events= 165 
       coef exp(coef) se(coef)      z Pr(>|z|)   
sex -0.5310    0.5880   0.1672 -3.176  0.00149 **  
---
Signif. codes:  0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1
    exp(coef) exp(-coef) lower .95 upper .95
sex     0.588      1.701    0.4237     0.816
Concordance= 0.579  (se = 0.022 )
Rsquare= 0.046   (max possible= 0.999 )
Likelihood ratio test= 10.63  on 1 df,   p=0.001111
Wald test            = 10.09  on 1 df,   p=0.001491
Score (logrank) test = 10.33  on 1 df,   p=0.001312

结果的各项指标解释如下：

Statistical significance. z值给出了Wald统计值。它对应于每个回归系数与其标准误差的比率（z = coef / se（coef））。 wald统计量评估给定变量的系数（β）是否在统计学上显著，由上可知，变量性别具有高度统计上显著的系数。
The regression coefficients. Cox模型结果中要注意的第二个特征是回归系数（coef）的符号。如果回归系数为正值，说明死亡风险高，预后差；为负值，则风险低，预后好。 R给出的是第二组相对于第一组的风险比（HR），即女性对男性。在这些数据中，性别的β系数= -0.53表明女性的死亡风险（低存活率）低于男性。
Hazard ratios. 指数系数（exp（coef）= exp（-0.53）= 0.59）也称为风险比，给出协变量的效应大小。例如，女性（性别= 2）的风险降低了0.59倍，即41％。女性与预后良好相关。
Confidence intervals of the hazard ratios. 给出了风险比（exp（coef））的95％置信区间的上限和下限。
Global statistical significance of the model. 三个检验模型的P值：The likelihood-ratio test, Wald test, and score logrank statistics.这三种方法是类似的，如果样本量足够大，则三个方法会得到相同的结果，当样本量较小时，The likelihood-ratio test能得到较好的结果。

多因素cox分析

res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data =  lung)
summary(res.cox)

Call:
coxph(formula = Surv(time, status) ~ age + sex + ph.ecog, data = lung)
  n= 227, number of events= 164 
   (1 observation deleted due to missingness)
             coef exp(coef)  se(coef)      z Pr(>|z|)    
age      0.011067  1.011128  0.009267  1.194 0.232416    
sex     -0.552612  0.575445  0.167739 -3.294 0.000986 ***
ph.ecog  0.463728  1.589991  0.113577  4.083 4.45e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
        exp(coef) exp(-coef) lower .95 upper .95
age        1.0111     0.9890    0.9929    1.0297
sex        0.5754     1.7378    0.4142    0.7994
ph.ecog    1.5900     0.6289    1.2727    1.9864
Concordance= 0.637  (se = 0.026 )
Rsquare= 0.126   (max possible= 0.999 )
Likelihood ratio test= 30.5  on 3 df,   p=1.083e-06
Wald test            = 29.93  on 3 df,   p=1.428e-06
Score (logrank) test = 30.5  on 3 df,   p=1.083e-06

由上可知：在三种检验方法中，p值都是显著的。这表明了该模型的重要性。

在多变量Cox分析中，协变量sex和ph.ecog仍然显着（p <0.05）。然而，协变量age并不显着（p = 0.23）。

sex的p值为0.000986，危险比HR = exp（coef）= 0.58，表明患者性别与死亡风险降低之间有很强的关系。协变量的风险比可以解释为对风险的倍增效应。例如，将其他协变量保持不变，即女性（sex= 2）可将风险降低0.58倍，即降低42％。我们的结论是，女性与良好的预后相关。
类似地，ph.ecog的p值为4.45e-05，危险比HR = 1.59，表明ph.ecog值与死亡风险增加之间的强关系。保持其他协变量不变，ph.ecog的较高值与生存率较差相关。
相比之下，age的p = 0.23。风险比HR = exp（coef）= 1.01，95％置信区间为0.99至1.03。由于HR的置信区间包括1，因此这些结果表明年龄在调整ph.ecog和sex后对HR差异的贡献较小，并且仅趋向于显着性。例如，将其他协变量保持不变，额外的一年会导致每日死亡风险的因数为exp（beta）= 1.01或1％，这不是一个重大贡献。

注意事项

年龄，作为连续变量，一般情况是默认服从比例风险假设的，可以直接进行回归分析。
单因素分析一方面可初步筛选出可能与预后有关的因素；另一方面去除那些根本不可能相关的因素，以减少建立多元回归模型时的“压力”。

References:

Cox Proportional Hazards Modelhttp://www.sthda.com/english/wiki/cox-proportional-hazards-model