lasso回归筛选构建生存模型
背景
在进行预后分析的过程中,往往会从大量的遗传特征中筛选有效的变量进行预后标志的构建。一般的构建过程会通过单因素cox和多因素cox等进行特征的过滤和变量筛选,然而这样的筛选过程有时候仍然会剩余较多的变量,这对后期预后标志的构建和使用会造成一定的困扰。因此需要一些更为有效的方法对得到的特征进行更加有效的过滤,其中lasso回归目前已经被广泛的运用到预后特征的筛选过程中。
lasso 回归
lasso(Least Absolute Shrinkage and Selection Operator)回归是一种正则化回归(regularized regression),它是在在最小二乘的基础上增加了一个罚分项来对估计参数进行压缩,当参数缩小到小于一个阈值的时候,就令它变为0,从而选择出对因变量影响较大的自变量并计算出相应的回归系数,最终能得到一个比较精简的模型。LASSO方法在处理存在多重共线性的样本数据时有明显的优势。
lasso回归简单的讲就是一种变量筛选的回归,保留最具影响力的变量,将其他影响较小的变量过滤掉。
LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选(variable selection)和复杂度调整(regularization)。因此,不论因变量(dependent/response varaible)是连续的(continuous),还是二元或者多元离散的(discrete),都可以用LASSO回归建模然后预测。这也是lasso可以运用于预后变量筛选的原因。
LASSO回归的复杂度主要由参数λ(lambda)来控制.lambda越大,对变量较多的线性模型的惩罚力度就越大.最终获得一个变量较少的模型。
另外还有一个参数α(alpha)用来控制高度相关性模型的性状。LASSO回归时,alpha设置为1。
lasso回归的R实现
lasso回归在R语言中可以使用glmnet包中的glmnet函数进行实现,该包同时还包含了岭回归、弹性网络回归的计算。
其常用的参数如下:
x: 自变量数据集,需要为matrix格式,行为观测值,列为变量。y: 因变量数据集,需要为matrix格式,只有一列。family: 应变量类型.如果时连续性变量(也就是要做回归分析),family应该为gussian(高斯分布/正态分布)或者poisson(泊松分布)。如果为二分类不连续变量(factor类型,且只有两个levels),应设置为binomial。如果为多分类不连续变量(factor类型,且多个levels),则应设置为multinomial。如果设置为cox,则y应当为一个两列的matrix,列名分别为time和status,time为存活时间,status为结局状态(1代表死亡,0代表还未死亡)。alpha: 在LASSO回归中,将其设置为1。nlambda: 选取多少个lambda进行优化,默认为100.也就是使用100个lambda值拟合出100个系数不同的模型。lambda: 提供lambda值,如果设置该值(一个或者多个),则会覆盖掉自动选择的lambda值。standardize: 是否对数据进行标准化(scale),默认为TRUE.如果自己做过scale标化,这里需要设置为FALSE。
lasso cox进行变量筛选
使用R包自带的数据进行操作:
## library package
library(glmnet)
## load example data
data(CoxExample)这个数据中共包含两个数据一个是包含30个基因在1000个病人样本中的表达矩阵,另一个是每个患者的生存状态和生存时间,生存时间以年为单位,如下:
head(x[,1:3])
## [,1] [,2] [,3]
## [1,] -0.8767670 -0.6135224 -0.56757380
## [2,] -0.7463894 -1.7519457 0.28545898
## [3,] 1.3759148 -0.2641132 0.88727408
## [4,] 0.2375820 0.7859162 -0.89670281
## [5,] 0.1086275 0.4665686 -0.57637261
## [6,] 1.2027213 -0.4187073 -0.05735193
head(y)
## time status
## [1,] 1.76877757 1
## [2,] 0.54528404 1
## [3,] 0.04485918 0
## [4,] 0.85032298 0
## [5,] 0.61488426 1
## [6,] 0.29860939 0
## reshape the data
rownames(x) <- paste0("patient", 1:1000)
colnames(x) <- paste0('gene', 1:30)
rownames(y) <- paste0('patient', 1:1000)
## Construct cox object
library(survival)
cox_fit <- Surv(y[, 'time'], y[, 'status'])
## lasso cox regression
fit <- glmnet(x, cox_fit, family = "cox")
## plot the picture
plot(fit, label = T)
lasso回归最重要的是选择合适的λ值,可以通过cv.glmnet函数实现
cvfit <- cv.glmnet(x, cox_fit, family = "cox", nfolds = 10)
plot(cvfit)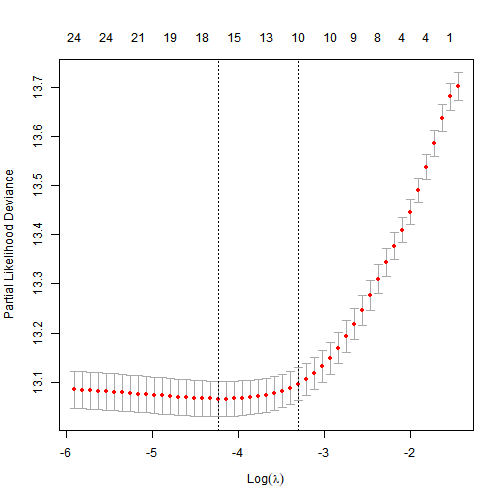
一般可以采用两个内置函数cvfit$lambda.min和 cvfit$lambda.1se提取最佳的lambda值
## choose the optimal lambda
cvfit$lambda.min
## [1] 0.01452734
cvfit$lambda.1se
## [1] 0.0368321保留lambda最佳值处的结果,采用coef函数提取具有系数的结果,即筛选之后的特征
fit_coef <- coef(cvfit, s = cvfit$lambda.1se)
fit_coef
## 30 x 1 sparse Matrix of class "dgCMatrix"
## 1
## gene1 0.41905187
## gene2 -0.12484193
## gene3 -0.16652849
## gene4 0.12790688
## gene5 -0.14144376
## gene6 -0.42771578
## gene7 0.27727379
## gene8 0.05780711
## gene9 0.38552188
## gene10 0.06912816
## gene11 .
## gene12 .
## gene13 .
## gene14 .
## gene15 .
## gene16 .
## gene17 .
## gene18 .
## gene19 .
## gene20 .
## gene21 .
## gene22 .
## gene23 .
## gene24 .
## gene25 .
## gene26 .
## gene27 .
## gene28 .
## gene29 .
## gene30 .
## extract genes
fit_out <- fit_coef[which(fit_coef != 0),]
fit_out
## gene1 gene2 gene3 gene4 gene5
## 0.41905187 -0.12484193 -0.16652849 0.12790688 -0.14144376
## gene6 gene7 gene8 gene9 gene10
## -0.42771578 0.27727379 0.05780711 0.38552188 0.06912816至此,筛选出最终需要保留的变量特征。