ROC曲线和AUC
ROC和AUC简介
ROC(Receiver Operating Characteristic)曲线和AUC常被用来评价一个二值分类器(binary classifier)的优劣,对两者的简单介绍见wiki百科这篇博文主要简单介绍ROC和AUC的特点,以及如何通过R语言绘制ROC曲线和计算AUC值。
ROC曲线意义
在这里,我们只讨论二值分类的情况,即“非此即彼”。一般对于二分问题来说,预测分类的结果有四种情况:
- 真阳性(TP):预测为正样本,真实也是正样本。
- 伪阳性(FP):预测为正样本,而真实是负样本。
- 真阴性(TN):预测为负样本,真实也是负样本。
- 伪阴性(FN):预测为负样本,而真实是正样本。 用列联表表示其结果,如下所示,1代表正样本,0代表负样本:
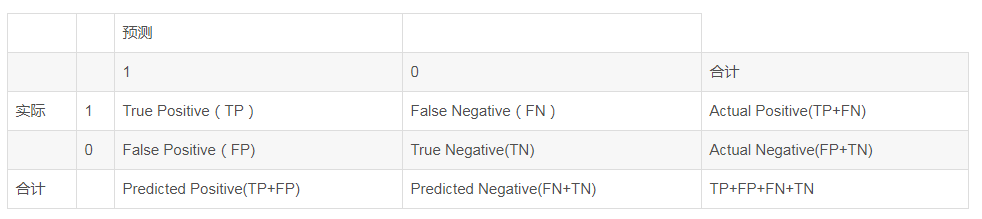
在这里需要引入两个名词: 真阳性率 (TPR, true positive rate) :又称:命中率 (hit rate)、敏感度(sensitivity) TPR = TP / P = TP / (TP+FN) 伪阳性率(FPR, false positive rate) :又称:错误命中率,假警报率 (false alarm rate) FPR = FP / N = FP / (FP + TN)
给定一个二元分类模型和它的阈值,就能从所有样本的(阳性/阴性)真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。如下图所示:
接下来,我们考虑ROC曲线图中的四个点和一条线。第一个点,(0,1),即FPR=0, TPR=1,这意味着这是一个完美的分类器,它能够将所有的样本都正确分类。第二个点,(1,0),即FPR=1,TPR=0,说明这个分类器完全无效能可言,将所有的样本都错误的分类。第三个点,(0,0),即FPR=TPR=0,说明所有的样本全是负样本。类似的,第四个点(1,1),分类器实际上预测所有的样本都为正样本。经过以上的分析,我们可以发现ROC曲线越接近左上角,说明分类器的分类效能越好。
下面考虑ROC曲线图中的虚线y=x上的点。这条对角线上的点其实表示的是一个采用随机猜测策略的分类器的结果,例如(0.5,0.5),表示该分类器随机对于一半的样本猜测其为正样本,另外一半的样本为负样本。
ROC曲线绘制原理
对于一个分类器来说,其特点是“概率输出”,即分类一个样本是根据这个样本有多大概率是正样本(或负样本)来确定的。因此当分类器模型的阈值变化时,样本的分类情况也会发生改变,每种阈值的设定会得出不同的FPR和TPR。将同一分类器模型每个阈值的 (FPR, TPR) 座标都画在ROC空间里,就成为特定模型的ROC曲线。
假如我们已经得到了所有样本的概率输出(属于正样本的概率),现在的问题是如何改变“discrimination threashold”?我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率

我们从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:

当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
AUC的意义
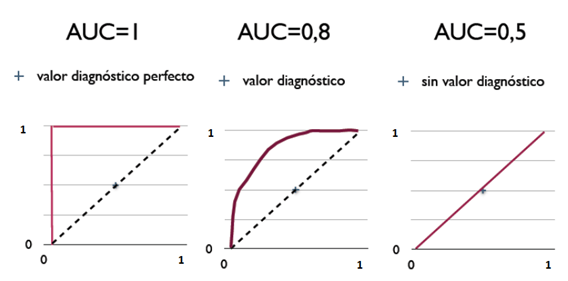
AUC(Area Under Curve),又称为曲线下面积,其意义为随机抽取一个阳性样本和一个阴性样本,分类器正确判断阳性样本的值高于阴性样本的机率。AUC值越大,说明当前分类器分类的正确率越高,分类器模型也就越好。
- AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
图形示例如下: